Making Platonic Solids Out of Paper
Feb 11, 2023 · 4 min read
The Wager That Started it All

A few months ago I was eating lunch with some friends when I wagered, “Do you think you could find the center of the base of this glass with nothing but a pencil and paper?” A little friendly competition then broke out. I thought nothing more of this silly challenge at the time, but what followed was a sudden interest (obsession?) in finding ways to draw shapes and analyze them without ever making a single measurement.
I ended up buying a cheap compass, found a straightedge, and started drawing circles. After some failed attempts at finding the center of a circle, I stumbled across a book called Euclid’s Elements online. For those of you who don’t know, Euclid’s Elements is a collection of books covering geometry, definitions, propositions, theorems, and more, written by an ancient Greek mathematician named Euclid. For any math enthusiasts out there, Euclid was describing the mathematical system now known as Euclidean geometry.
Boring math background aside, after spending some time exploring Euclid’s Elements I eventually learned a way to find the center of a circle with nothing but pen, paper, and a straightedge. I had solved the problem! Slowly, Euclid started to slip away, and I forgot all about his propositions; months passed and that was the end of that. Or was it?
My Lazy Day
Flash forward to this past week. I had a day when I didn’t feel like doing anything. I was burnt out and tired. Usually when that happens, I try to block off an hour or two in the afternoon to relax and just reset. This time I decided to do something creative 😲
I was sitting at my desk thinking what to do. That’s when Euclid popped into my head for the first time in months. “I should start drawing fun shapes again” I thought. And I did just that for a bit, but ultimately I wanted more. I wanted to move to three dimensions. In that moment I realized that I can use Euclid’s first proposition from Book 1 – to construct an equilateral triangle on a given finite straight line – in a new way. The regular triangles I make could form a net that I could then cut out to form cool 3D shapes. I decided to start with some well known ones, the Platonic Solids.
The Platonic solids are five regular, three dimensional polyhedrons. Since I was limiting myself to just triangles, I set out to make the tetrahedron (4 sides), octahedron (8 sides), and icosahedron (20 sides). On a side note, the cube (6 sides) and dodecahedron (12 sides) require squares and pentagons respectively to construct. Euclid does have propositions for drawing regular squares and pentagons inside of circles, but these are much more involved and complicated. So for now, I focused just on the solids made up of regular triangles.
Let’s Make Them!
Here’s what I did. I got a cutting mat, paper, scissors, straightedge, tape/glue, compass, and a blunt letter opener to make it easier to fold the paper.

Then I got to work. Using Euclid’s first proposition, I constructed an equilateral triangle. Then I added a third circle to form four equilateral triangles. The red triangles below form the net of a tetrahedron.
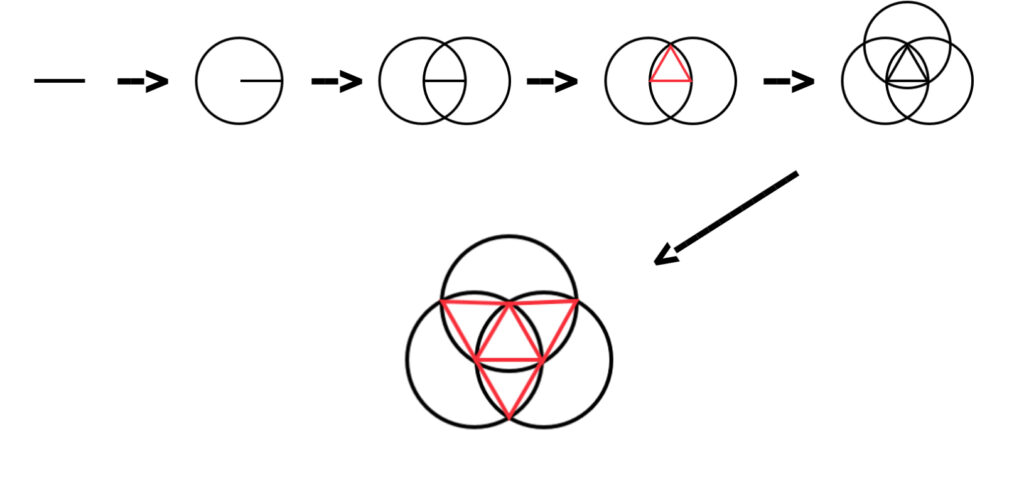
All that was left was to cut out the net and fold it. The exact same process can be followed to create the octahedron and dodecahedron, albeit a little more complex (but the idea is the same). At the end of the day, I had three paper Platonic solids and my burnout was gone! 😄

For those of you interested I’ve included the nets and outlines for all three solids below:
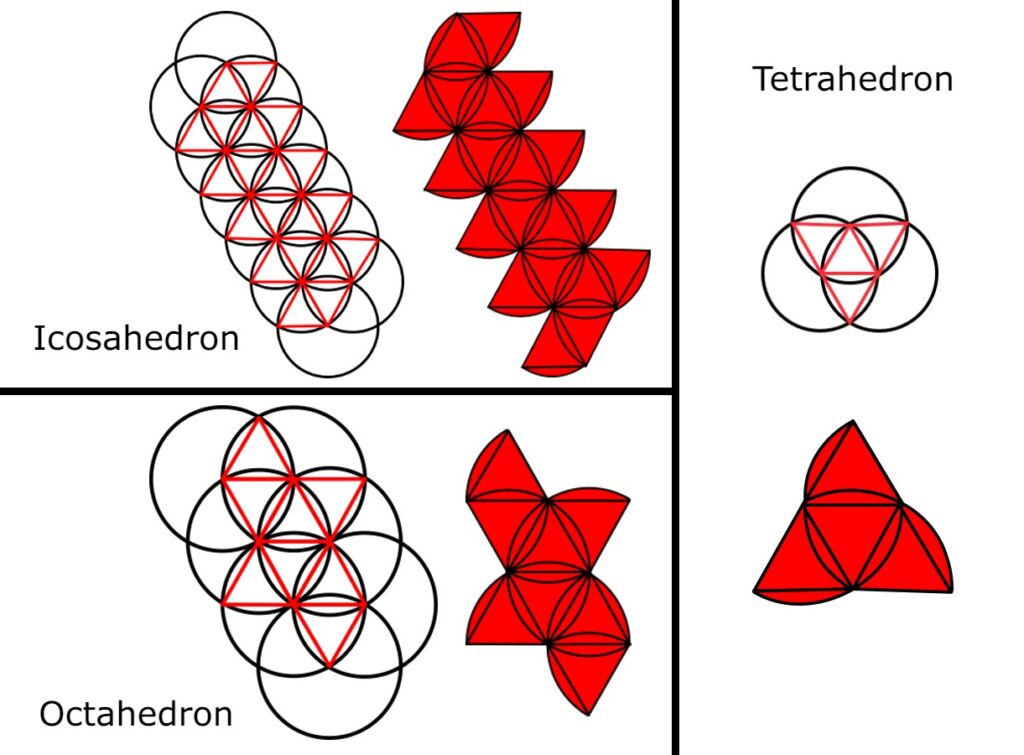
You may notice there are curved pieces on some of the sides on the cutouts. Because I was dealing with paper I would need to glue the sides together, these flaps helped hold the shape together by providing a place to add glue.
Make Them Yourself
And that’s all! Let me know in the comments if you try this method to make these yourself! Alternatively, I’ve provided printouts of the nets I used! You can download each image down below, then just print, cut out, fold, and glue them together to make your own Platonic solids.
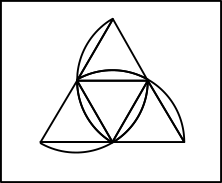
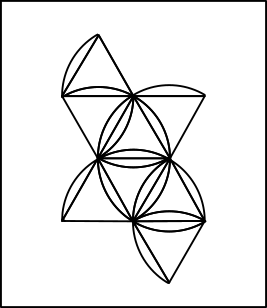
Leave a Reply