The Fundamental Theorem of Arithmetic states that any positive integer greater than 1 can be expressed as a product of prime numbers and that this product is unique.

A prime number is any number that is divisible only by 1 and itself. For example, the first few primes are:

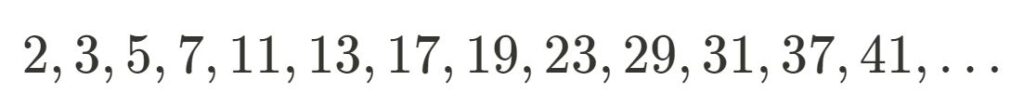
Let us now return to The Fundamental Theorem of Arithmetic (FToA) and break it down. The first half states: Any positive integer greater than 1 can be expressed as a product of prime numbers. Let’s look at this first part in detail using a few examples.

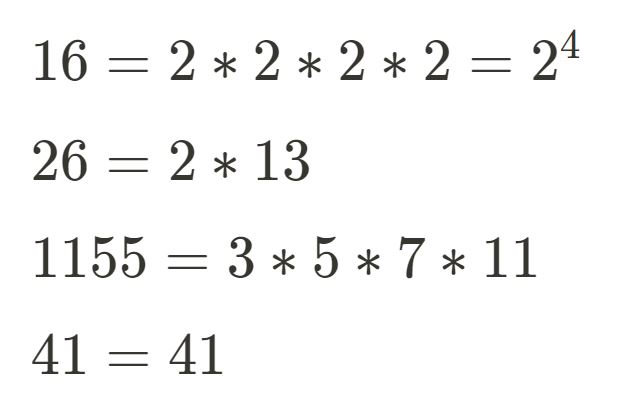
We see each integer above is “broken down” into its prime factor components. This process is also known as prime factorization. The second half of the FToA is by far the most interesting: The prime factorization of any integer greater than 1 is unique. Think about that for a moment. The only way to write 26, for example, as a product of prime numbers is ONLY by multiplying one 2 with one 13. There is no other way to write it otherwise. This is incredibly important as we can now think of prime numbers as the fundamental building blocks of whole numbers. Any composite number, a number that isn’t prime, can be uniquely broken down into a product of prime numbers. The prime number has become the indivisible unit we use to construct composite numbers.

A Mathematical Building Block

Let’s look at an analogy to prime numbers by turning shortly to the world of Chemistry. It’s well known that all molecules are made up of some fundamental building block. In chemistry, those units are the elements and each molecule has a unique elemental composition (molecules are actually more complicated than that because chemical properties are not only dictated by their composition of elements but also their spatial arrangement).

In 1869, Dimitri Mendeleev successfully organized the elements into the now familiar Periodic Table of the Elements. As of today, there are 118 known, unique elements in existence and these 118 make up every known molecule in the universe. Therefore, we can think of prime numbers as our “mathematical elements” and composite numbers as our “molecules”.

Naturally, one may wonder since there is a finite number of elements in the Periodic Table, are there, then, a finite number of prime numbers? The answer to that is no, there is an infinite number of prime numbers. Proving this statement goes back to Euclid around 300 BC. If you’re interested in this proof, I’ve linked it here but we won’t go into detail now.

Conclusion

Quickly, let’s summarize everything covered so far:

• The Fundamental Theorem of Arithmetic states that any positive integer greater than 1 can be expressed as a product of prime numbers and that this product is unique
• Prime numbers are the indivisible building blocks of composite numbers
• There is an infinite number of prime numbers

I want to go back to our chemistry analogy for a second. Everything in our known universe is made up of 118 different elements, and that is rather incredible considering how much stuff simply exists. Now, turning to mathematics and the prime numbers, just try to imagine for a second how many composite numbers you can create using 118 unique primes; now imagine using an infinite number of primes to do so. That’s a huge number and, chances are, you’ve barely even gotten close to using all of our infinite unique primes. For me, this puts the sheer size of infinity into the tiniest speck more perceptible than otherwise.

I hope by sharing The Fundamental Theorem of Arithmetic and its analogy to chemistry I was able to bring mathematics out of the abstract and into something more tangible for you. If you enjoyed it, please consider checking out some of my other articles below and stay tuned for more math-related content!

** There are also a number of important consequences of the FToA, ranging from number theory to cryptography, that I didn’t cover in this article. If you’re interested in a proof of the FToA, click here.