Ulam Spiral: Patterns in the Primes
July 6, 2023 · 6 min read
“The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas, like the colours or the words must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics.”
G. H. Hardy
Introduction
Prime numbers have found a plethora of applications in areas such as telecommunications and networking, security, cryptography, and of course mathematics and number theory. Because of their usefulness, it’s no wonder mathematicians everywhere have been tirelessly working to find a pattern — or put another way some formula — to generate every single prime number in existence. Such a pattern would be incredibly useful. For example, it could quickly tell you if 1,678,551 is prime or not (it’s not) and it could easily generate a prime number with millions of digits.
In this article, we are setting forth on the hunt to find patterns in the humble set of primes, but before doing so let’s briefly review some important definitions. Recall, a prime number is any number that has exactly two distinct numbers that divide it, these divisors are 1 and itself. A composite number is any number that is the product of two or more prime numbers. We are now equipped to revisit the list of the first few prime numbers:
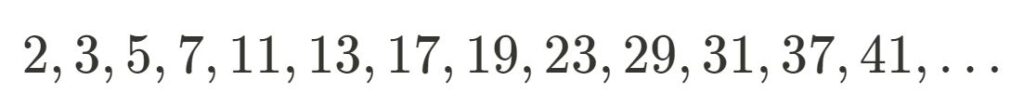
After staring at this list long enough, you may start to question if any discernable pattern between prime numbers actually exists. After all, their order seems so random. Nevertheless, let’s see what immediate observations we can make.
First, observe that 2 is the only even prime number. That’s pretty interesting, but it makes sense when you think about it because all even numbers are, by definition, divisible by two. From this, it follows that no prime number, besides 2, can end in 2, 4, 6, or 8.
Second, notice that no prime number, besides 5, ends in a 5. Again this makes sense once you realize that any number ending in 5 must be a multiple of five.
Finally, it’s apparent that no primes can be multiples of 10. This follows logically from our previous two observations, as that would imply they are divisible by both 2 and 5 (since 10=2*5), so no primes end with a 0.
We’ve made some decent observations and we can certainly make more, such as writing down the relative density of primes or their relative differences, but you’ll find that also leads us nowhere. So the question still remains, can we find beautiful, aesthetic patterns in the prime numbers?
The Ulam Spiral
Our first hope for finding patterns in the primes begins in 1963 when a Polish mathematician named Stanisław Ulam was sitting through a rather dull scientific meeting. Bored, Ulam began to doodle on some scratch paper. Starting with the number 1 in the center of his page, he arranged the remaining positive integers around in a square spiral as shown below. Then, he marked which of these numbers were prime.

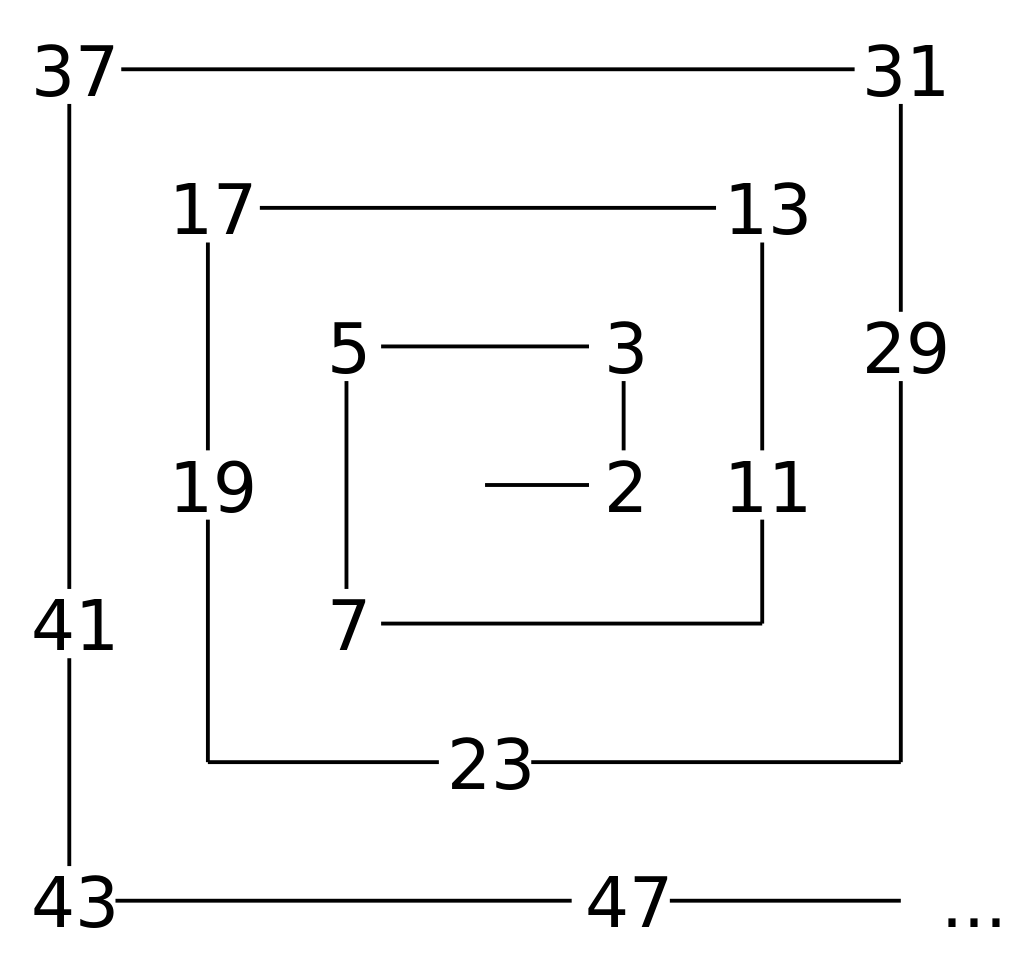
(Images courtesy: Wikipedia)
This arrangement of identifying primes among the positive integers has come to be known as an Ulam Spiral. At first, it doesn’t look all that interesting but that’s because it’s difficult for the eye to immediately spot any patterns. So, let’s abstract the numbers away, replace them with simple shapes, and make the spiral bigger by including more numbers. Below is an Ulam spiral where the primes are represented by black squares and composite numbers are left blank. The number 1 is colored in red to make it easier for the eye to find the center of the image. In this example, the first 625 positive integers are shown and 114 prime numbers are marked.

Already this is looking much better, but even with 625 integers, it’s difficult to see any noticeable patterns. Thankfully, with the help of computers, we can generate much larger spirals. Hopefully, that will help…
Patterns in the Primes
We’re now nearing the end of our quest to discover patterns in the set of primes. What follows is an Ulam Spiral of the first 62,500 positive integers with about 6,275 prime numbers marked.

Squint, zoom in, zoom out, or just stare at this for a few seconds, you may be surprised to see horizontal, vertical, and diagonal lines with a high density of prime numbers showing themselves! This is, in my opinion, a really cool revelation.
The Ulam Spiral shows us areas with a high density of prime numbers (for example, the prominent, diagonal dark “line” slightly above the center) and areas poor in prime numbers (for example, the vertical, empty “gap” right below the center). In fact, the lines with a high density of prime numbers are not random at all, they actually represent prime-generating polynomials (functions of the form x2+bx+c, where b and c are constants, that generate a prime number for some input x). A well-known example of this is Euler’s prime-generating polynomial x2–x+41 which generates a prime number for any integer x between -40 and 39 inclusive.
To illustrate that these patterns are not random, below is a spiral with odd numbers randomly colored black next to an Ulam Spiral of the same size.


(Images courtesy: Wikipedia)
This makes it pretty clear that there is some structure to the set of prime numbers.
Conclusion
Finding a single pattern or polynomial function that generates an infinite number of primes remains unsolved to this day and is an ongoing area of mathematical research. There is a lot of mystery still surrounding prime numbers, but I hope this article has shown you a glimpse of the beauty that can be found in mathematics. It’s satisfying, aesthetic, and, let’s be honest, there’s a certain excitement to exploring a problem that’s been unsolved for hundreds of years.
I hope you’ve enjoyed learning about the Ulam Spiral. If you want to download a high-resolution Ulam Spiral of 1 million positive integers and about 78,498 prime numbers marked, I’ve included a download link below. Let me know in the comments below if you find any really cool patterns!
** There are many variations of Ulam’s Spiral that I won’t go into detail here, but for those interested some examples include Klauber’s Triangle and the Sacks Spiral.
Acknowledgments
All Ulam Spiral images, unless otherwise stated, were generated using code adapted from The Coding Train. Special thanks to them for inspiring parts of this article!
Like what you read? Check out some of my other articles below:
- “Chemistry and The Fundamental Theorem of Arithmetic” – An introduction to The Fundamental Theorem of Arithmetic and, in an attempt to help readers understand, I provide an analogy to chemistry.
- “Making Platonic Solids Out of Paper” – A story about how I exercised my creativity and made the platonic solids out of paper using Euclid’s Elements.
Have a question? Leave a comment down below and I’ll try my best to answer it!
Leave a Reply